(ii) The average value of sin(mx)cos(nx) over a period is zero Z π −π sin(mx)cos(nx)dx = 0 (iii) The average value of sin(mx)sin(nx) over a period, Z π −π sin(mx)sin(nx)dx = ˆ π if m = n 6= 0 0 otherwise (iv) The average value of cos(mx)cos(nx) over a period, Z π −π cos(mx)cos(nx)dx = 2π if m = n = 0 π if m = n 6= 0 0 if m 6= n Remark The following trigonometric identitiesA 1 m long piece of wire is cut into 2 pieces one How manyIf the sum of the roots of the equation sin 2 θ = k, (0 < k < 1) lying in 0, 2 π is equal tothe sum of the angles of a nsided regulain polygon, then the value of n is Medium View solution

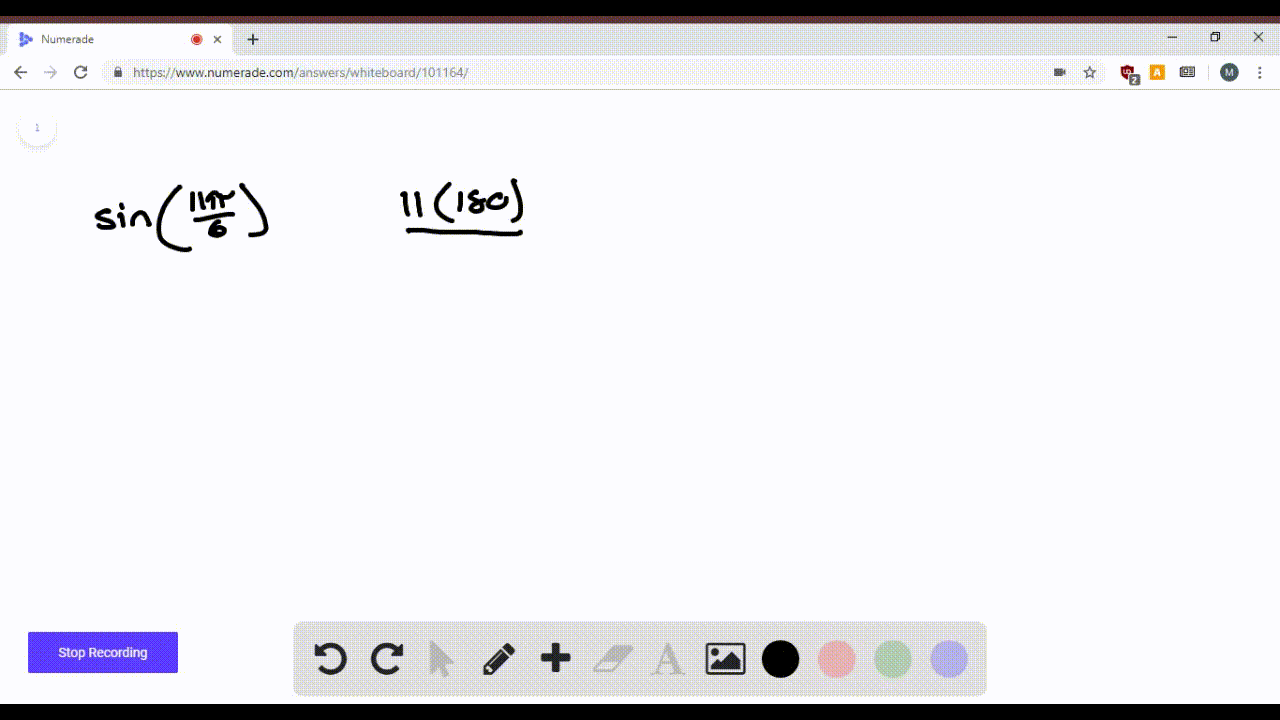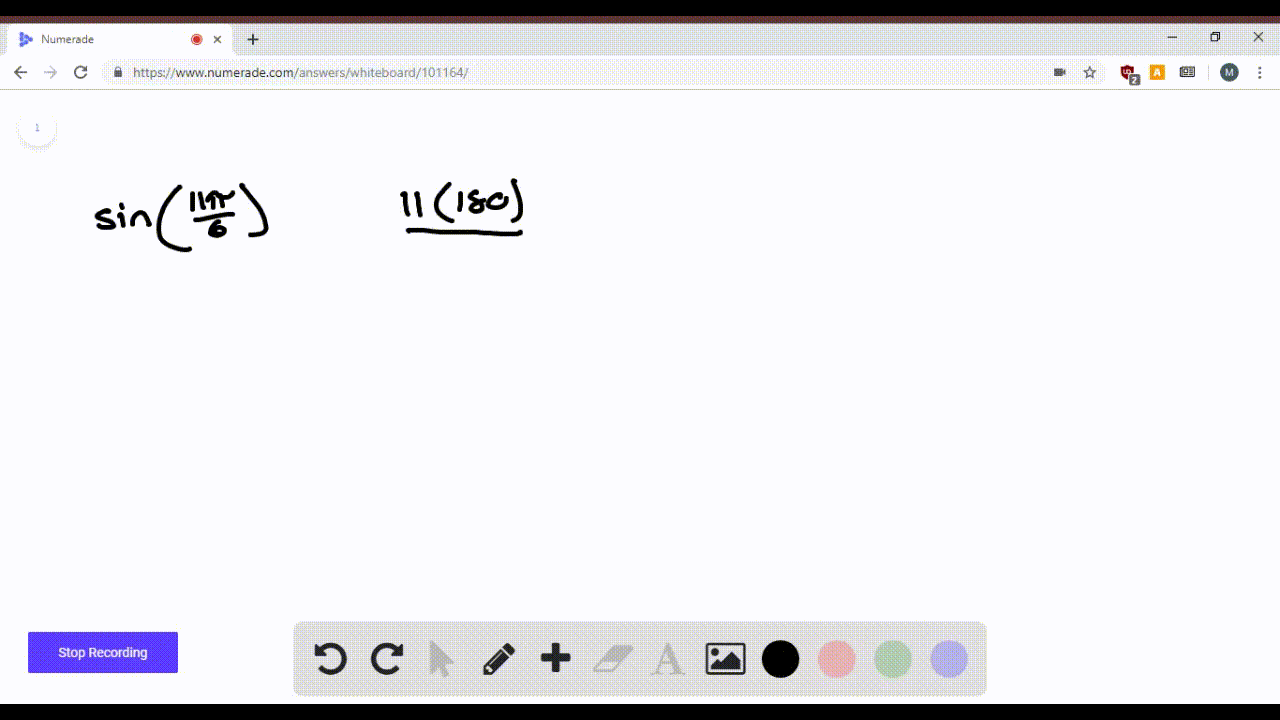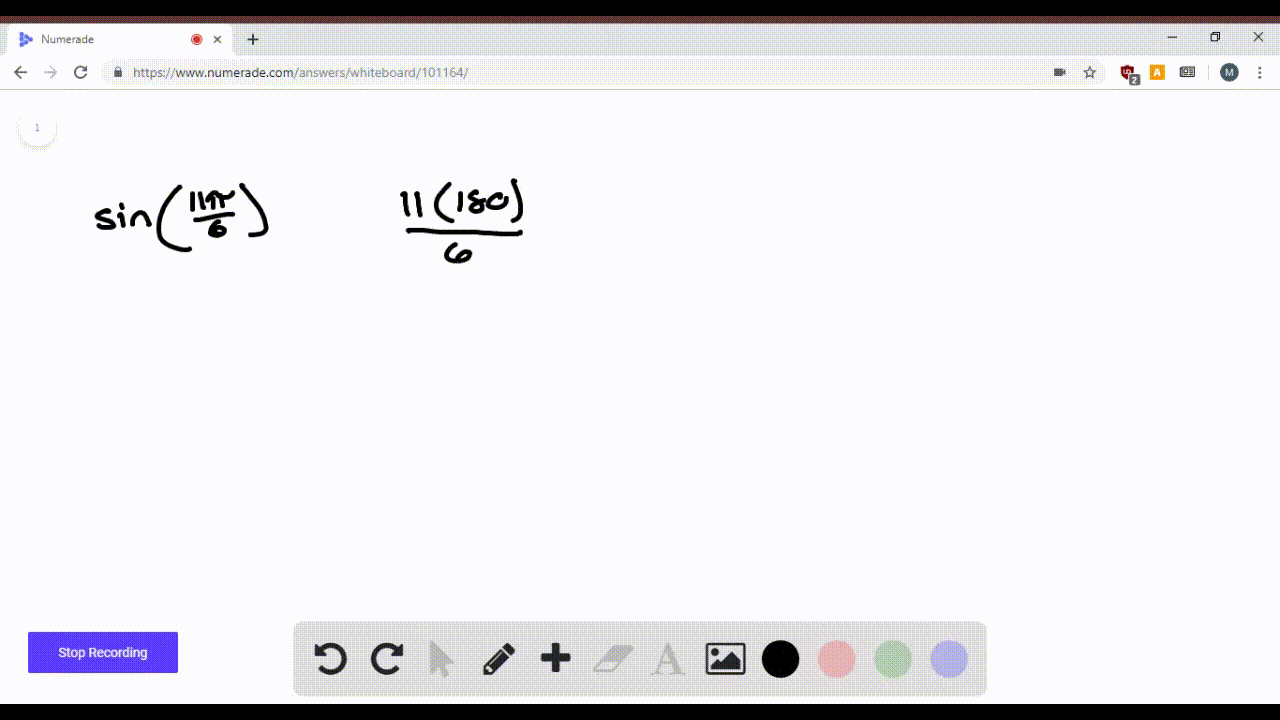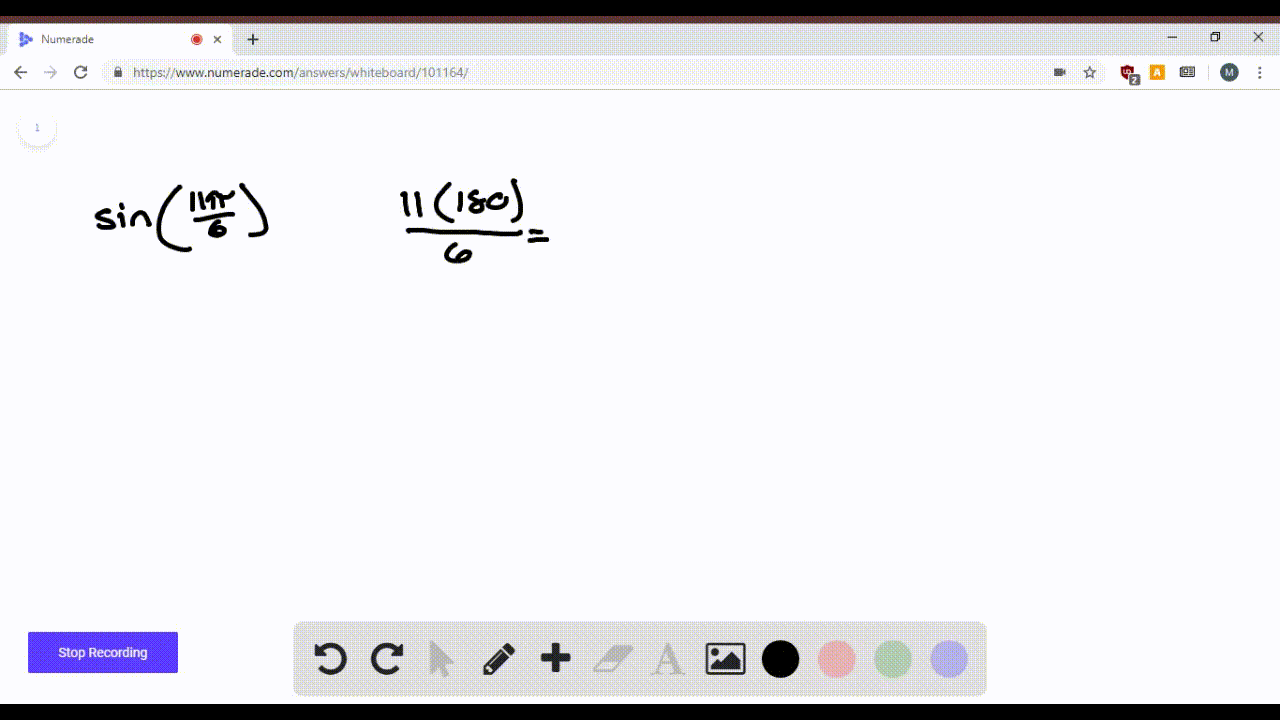
Find The Value Of Sin 11 Pi 3 Mathematics Stack Exchange
π/2 value
π/2 value-24/01/19 · What about the value of tan(π/2)?RMS value d θ π θ π 2 2 0 sin2 2 1 2 = − − − = − 2 sin0 0 2 sin4 2 2 1 2 π π π π π 2 2 1 2 = 7071V 2 100 = = Please note Being a sinusoidal wave, we can calculate the RMS value for this voltage using the relation derived on page1, ie vRMS=07×vpeak ⇒ vRMS=07×100≈7071V But it is not so straightforward in case of a nonsinusoidal function as



Given That Sin Theta 1 4 0 Theta P 2 What What Is The Exact Value Of Cos 8 Brainly Com
Find the Value of K If F(X) is Continuous at X = π/2, Where F ( X ) = { K Cos X π − 2 X , X ≠ π / 2 3 , X = π / 2 CBSE CBSE (Commerce) Class 12 Question Papers 1786 Textbook Solutions Important Solutions 3417 Question Bank Solutions 153 Concept Notes & Videos 440 Time Tables 18 Syllabus Advertisement Remove all ads Find the Value of K If F(X) is Continuous at Xπ/2 x=0 = 1 2 05 Example Find the volume of the solid bounded above by the plane z = 4 − x − y and below by the rectangle R = {(x,y) 0 ≤ x ≤ 1 0 ≤ y ≤ 2} Solution The volume under any surface z = f(x,y) and above a region R is given by V = ZZ R f(x,y)dxdy In our case V = Z 2 0 Z 1 0 (4−x−y)dxdy = Z 2 0 h 4x− 1 2 x2 −yx i 1 x=0 dy = Z 2 0 (4− 1 2 −y)dy = " 7y 226/09/11 · By the Mean Value Theorem, if f is continuous on a, b and differentiable on (a, b), (f(b) f(a))/(b a) = f'(c) for some c with a < c < b (*) Let f(t) = tan t, a = 0, and b = x Then the derivative of f(t), f'(t), is (sec t)^2, so (*) becomes (tan x)/x = (sec c)^2, for some c with 0 < c < x < π/2 However, sec t exceeds 1 on (0, π/2), so (sec c)^2 > 1 This means that (tan x)/x > 1, so
How do you know if #sin 30 = sin 150#?02/05/14 · Evaluate I = 0∫π/2 sin 4 cos 5 x dx Solution 12 13 a Notice that 2m 1 = 3 → m = 2 & 2n 1 = 2 → m = 3/ 2 I = (1 / 2) B( 2 , 3/2 ) = 8/15 b I = (1 / 2) B( 5/2 , 3 ) = 8 /315 Example(5) a Evaluate I = 0∫π/2 sin6 dx b Evaluate I = 0∫π/2 cos6 x dx Solution a Notice that 2m 1 = 6 → m = 7/2 & 2n 1 = 0 → m = 1/ 2 I = (1 / 2) B( 7/2 , 1/2 ) = 5π /32 b I = (110/02/16 · How do you find the value of #cot 300^@#?
15/04/19 · The value of cos π/2 2 cos π/2 3 cos π/2 10 sin π/2 10 is (1) 1/2 (2) 1/256 (3) 1/1024 (4) 1/512 jee mains 19;Share It On Facebook Twitter Email 1 Answer 1 vote answered Apr 15, 19 by Farhat (778k points) selected Apr 16, 19 by Vikash Kumar Best answer The correct option is (4) 1/512 Explanation ← Prev Question Next Question → Related questions 0Notice that as the angle gets larger and approaches π/2 rads, the opposite side gets larger and the adjacent side shrinks to 0 This means that tan(π/2) is equal to the expression 1/0 Division by 0 is undefined, so the function tan(π/2) is undefined and has no accepted value Conceptualizing angle measurements in terms of radians



39 The Value Of Sin Frac Pi 18 Sin Frac
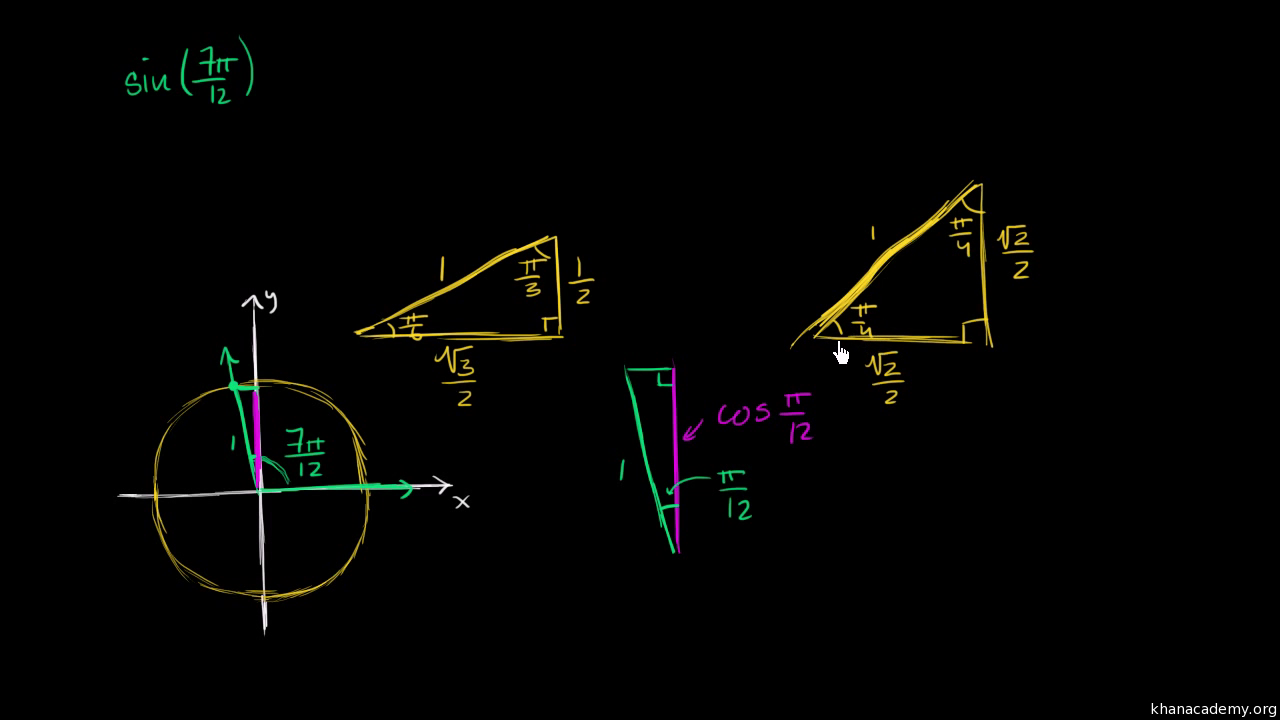


Finding Trig Values Using Angle Addition Identities Video Khan Academy
That is because some inverses work only with certain values Example Square and Square Root When we square a negative number, and then do the inverse, this happens Square (−2) 2 = 4 Inverse (Square Root) √(4) = 2 But we didn't get the original value18/08/01 · The trigonometric function are periodic functions, and their primitive period is 2 π for the sine and the cosine, and π for the tangent, which is increasing in each open interval (π /2 k π, π /2 (k 1) π) At each end point of these intervals, the tangent function has a vertical asymptote11/09/18 · If π = 314, then the value of π2 is (a) (b) 9860 (c) 986 (d) 99 7 Which of the following pairs of physical quantities have same dimension?



Ex Sine And Cosine Values Using The Unit Circle Multiples Of Pi 6 Radians Youtube
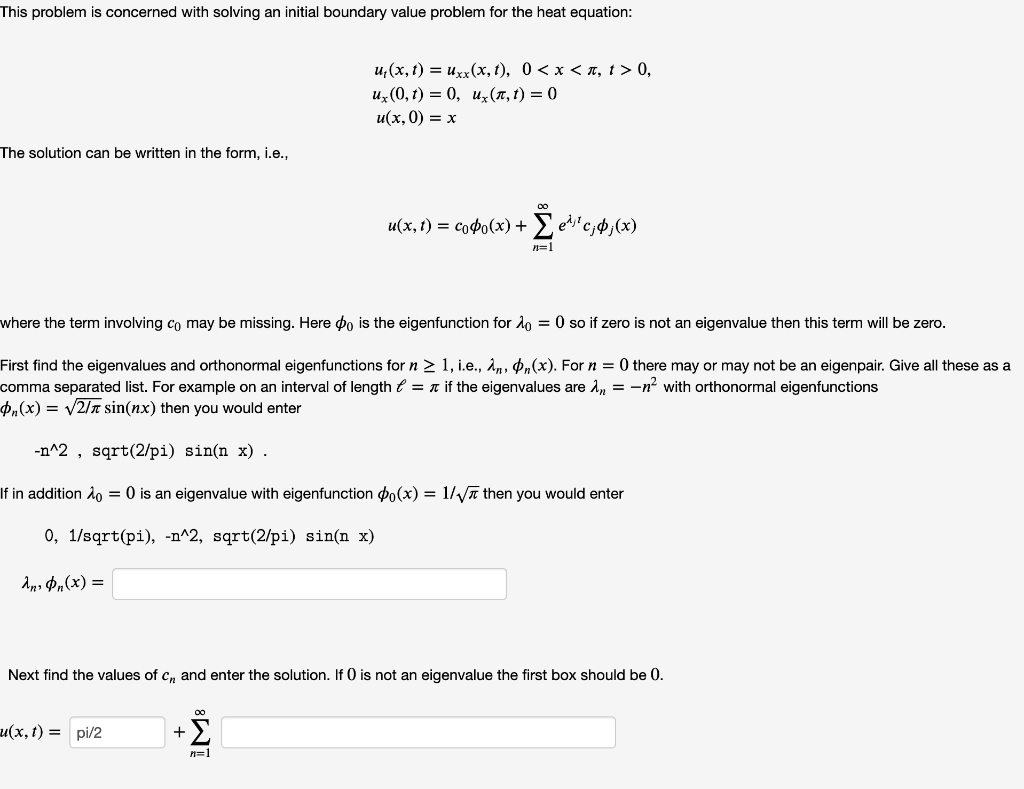


Solved This Problem Is Concerned With Solving An Initial Chegg Com
π^2/2 s Question 10 SURVEY Ungraded 30 seconds Report an issue Q What is the value of a0 if the function is f(x) = x3 in the interval 0 to 5?Function g is a cosine function and is therefore continuous on the interval π/2 , 3π/2 and differentiable on the interval (π/2 , 3π/2) Also g( π/2) = g(3π/2) = 0 and therefore function g satisfies all three conditions of Rolle's theorem and there is at least one value of xThe wave function of a certain particle is φ=A cos 2 (x) for π/2
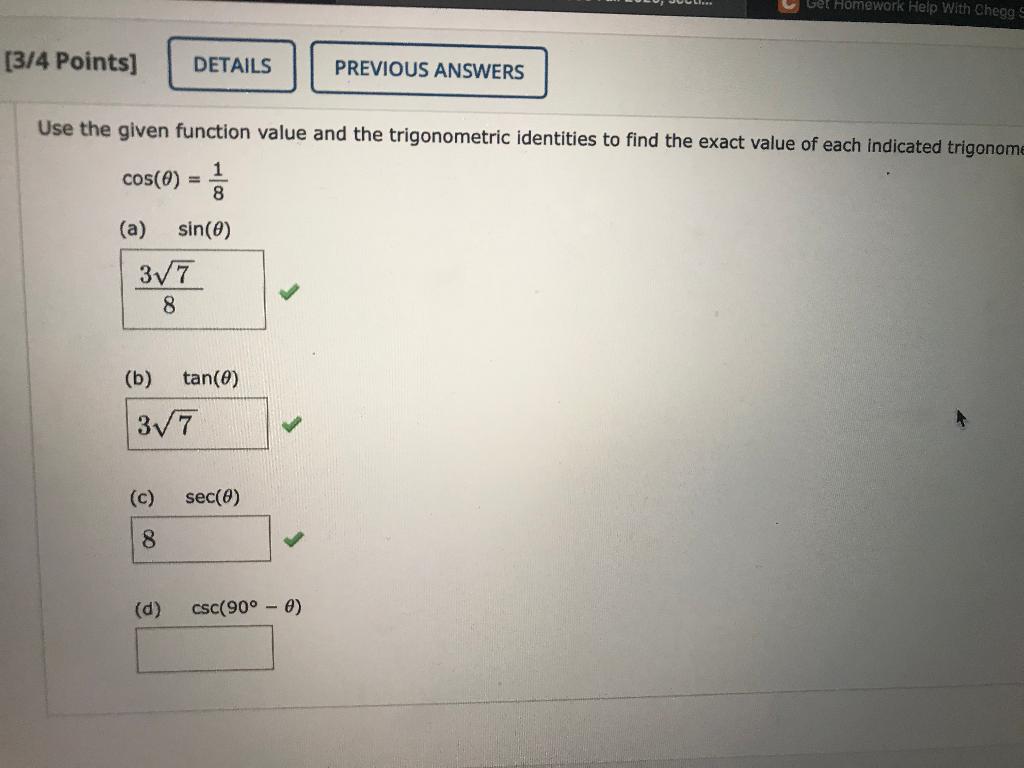


Solved Use The Given Function Value And The Trigonometric Chegg Com
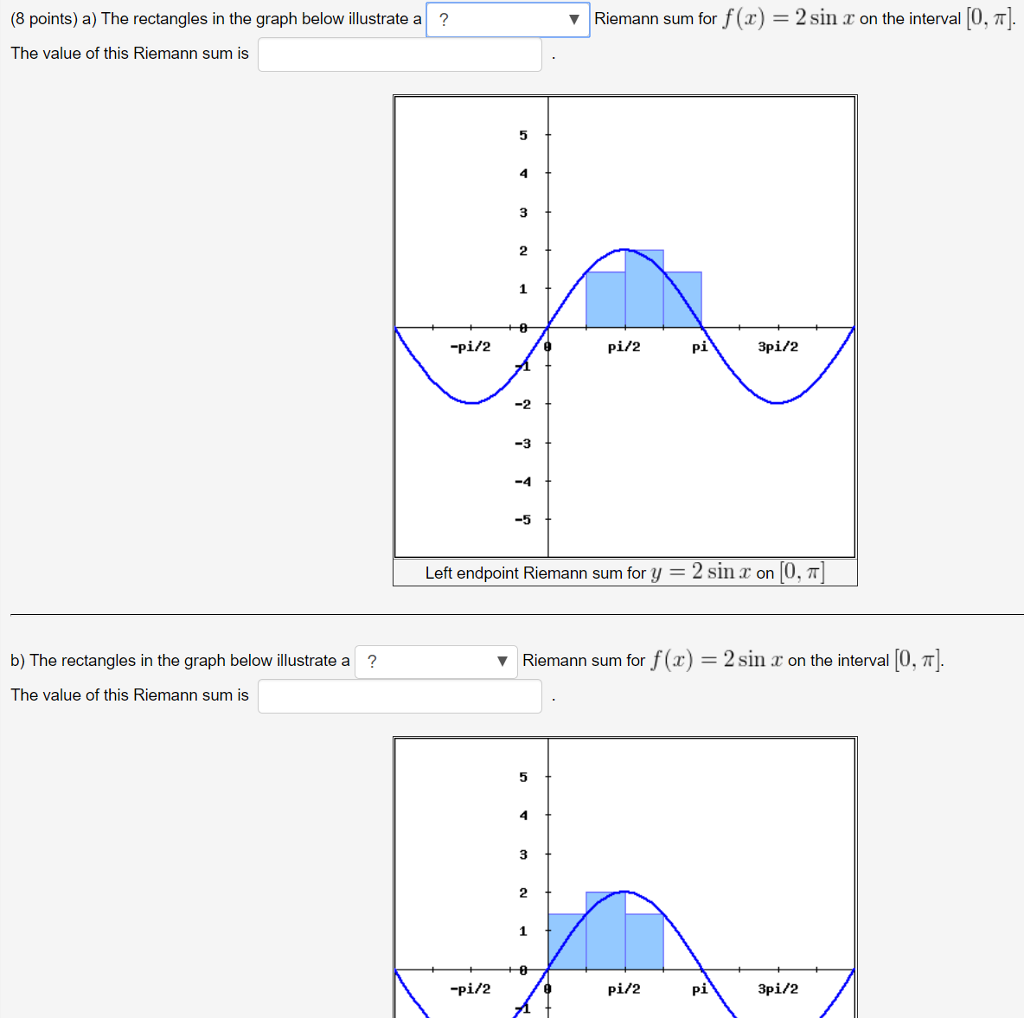


Solved Riemann Sum For F Z 2 Sin R On The Interva Chegg Com
For x ≠ π/4, find the value which can be assigned to f(x) at x = π/4 so that the function f(x) becomes continuous every where in 0, π/2 Advertisement Remove all ads Solution Show SolutionWhat is the value of #sin 45^@#?0 = π/2, halfway from 0 to π Ramp series RR(x)= π 2 − π 4 cosx 12 cos3x 32 cos5x 52 cos7x 72 ··· (15) The constant of integration is a 0 Those coefficients a k drop off like 1/k2Theycouldbe computed directly from formula (13) using xcoskxdx, but this requires an integration by parts (or a table of integrals or an appeal to


Solved 13 36 Values Of Trigonometric Functions F



If Cos8 12 13 0 Lt 8 Lt P 2 Find The Value Of Sin2 8 Cos2 8 2 Sin 8 Cos 8 1 Tan2 8 Brainly In
Answer choices 25/4 125/4 625/4 5/4 25/4 alternatives 125/4 625/4 5/4Use this simple sine calculator to calculate the sine value for π/2 in radians / degrees The Trignometric Table of sin, cos, tan, cosec, sec, cot is useful to learn the common angles of trigonometrical ratios from 0° to 360° Select degrees or radians in the drop down box and calculate the exact sine π/2 value easilyThe next value with an odd denominator is π /257 and the exact expression for cos(π /257) using squareroots only will be even more complicated!
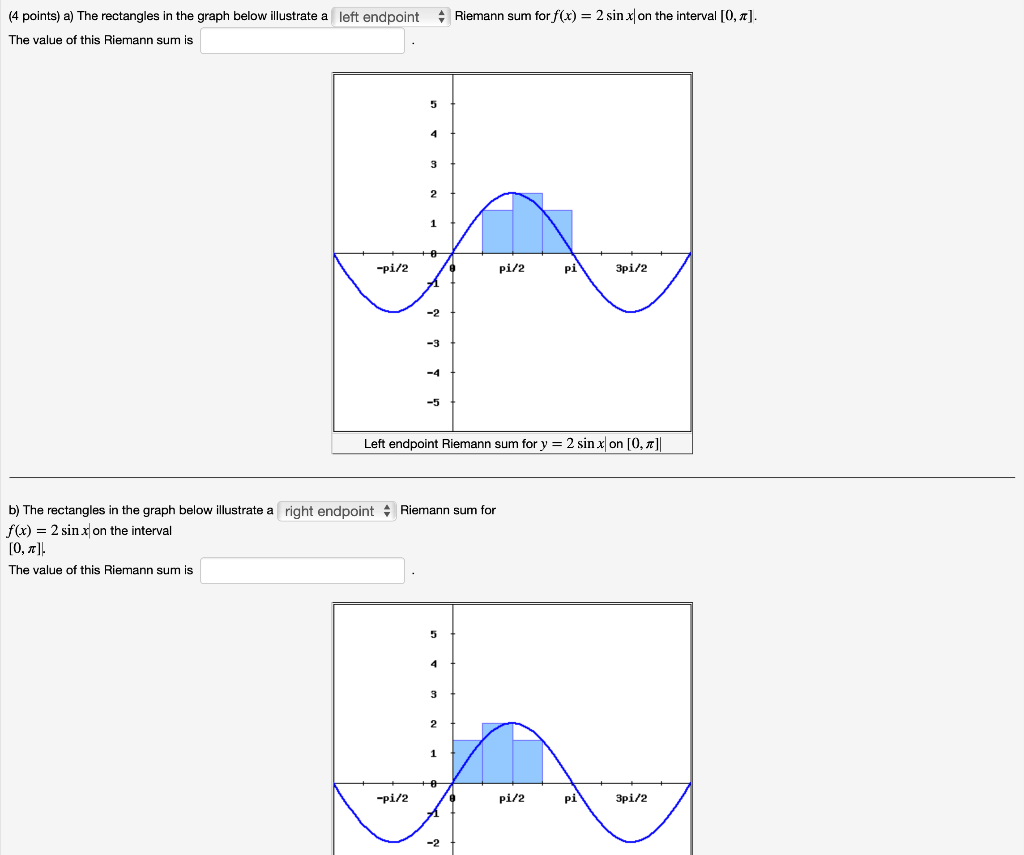


Solved Riemann Sum Forf X 2 Sin Xl On The Interval 0 Chegg Com



Solved Consider The Function Below F X 2x Tan X Pi Chegg Com
Cos π/2 Value in Radians / Degrees Cos Values for π/2 Use this simple cos calculator to calculate the cos value for π/2 in radians / degrees The Trignometric Table of sin, cos, tan, cosec, sec, cot is useful to learn the common angles of trigonometrical ratios from 0° to 360° Select degrees or radians in the drop down box and calculate the exact cos π/2 value easily α cos (αThe tangent to the curve at P cuts the yaxis at A, b) use calculus to find the coordinates of Aθ = π 2, respectively The contour integral can be evaluated as Z C z2 dz = Zπ 2 π ieiθ dθ = eiθ π 2 π = 1 i The results in (a) and (b) do not agree Hence, the value of this contour integral does depend on the path of integration 13
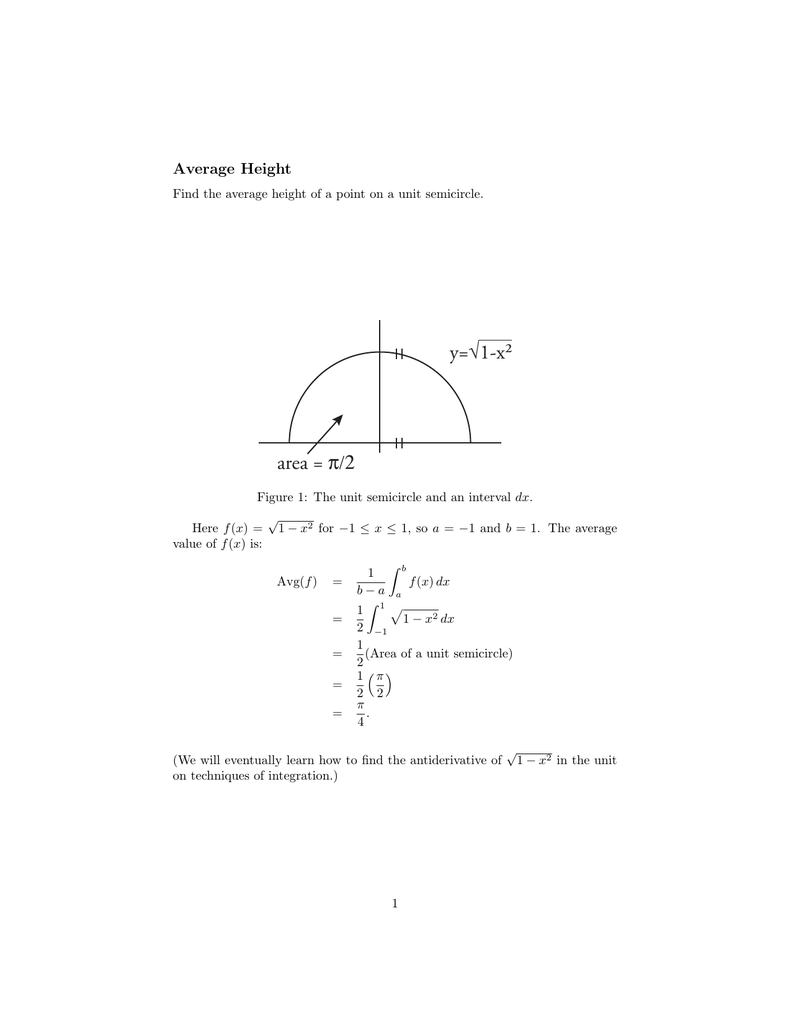


Y 1 X Area P 2 Average Height



Sin Pi 2 X Cot Pi 2 X Sinx Trigonometric Identities With Related Acute Angle Youtube
Textbook solution for Glencoe Algebra 2 Student Edition C14 1st Edition McGrawHill Glencoe Chapter 12 Problem 25SGR We have stepbystep solutionsPi^2 is numerically close to the value of g in m/s^2, but they have nothing to do with each other it is an entirely accidental coincidence Also it is convenient to remember that the number of seconds in a year is very close to pi times 10^7, but this too is a entirely accidental 545 views13/02/ · Transcript Example 9 Find the value of sin−1 (sin 3π/5) Let y = sin−1 ("sin " 3π/5) sin y = sin (3π/5) sin y = sin (108°) But, range of principal value of sin−1 is (−π)/2, π/2 ie −90° ,90° Hence, y = 108° not possible Rough 3𝜋/5 = (3 × 180)/5 = 108° Now, sin y = sin (108°) sin y = sin (180° – 72°) sin y = sin (72°) sin y = sin ("72 × " 𝜋/180) sin y



Solved For X 0 7854 And N 4 The Values Are Y 0 Sin Chegg Com



Value Of Tan Pi 2 Mathematics Stack Exchange
How do you find the trigonometric functions of values that are greater than #360^@#?Cos(2n1)π/2 is always zero when n€I For eg When n=1 Cos(21)π/2= cos3π/2 = cos270° which equals to 0 When n=2 Cos(41)π/2= cos5π/2= cos450° = Cos()°=cos90°=0 When n=1 Cos(21)/π/2 = cos(π/2) = cos(90°) =Cos(90°) = 0 Hence cos(2n1)π/ Please enable Javascript and refresh the page to continueFor any value of x between 1 and 1, the arcsine function returns a value between π/2 and π/2 radians (or 90⁰ to 90⁰) For example, when x=1, y=arcsine(x) returns y= π/2 radians This means that sin(π/2) = 1 If the arcsine graph is compared to the sine graph, one would see that the arcsine graph can be obtained from the sine graph by simply interchanging the horizontal and vertical



List Of Trigonometric Identities Wikipedia



The Value Of Int Pi 2 Pi 2 Sin 2x 1 2 X Dx Is A Pi
The lowest value among these values is the absolute minimum Absolute maximum 3sqrt(3)/2 Absolute minimum 0 1 keywords cos,sin,pi,F(t) = 2 cos t sin 2t, 0, π/2 Related Find all solutions in the interval 0, 2pi for si PreCalculus help please Solve sin x 2 sin&sup Spider!Let f(x) = (k cos x)/(π 2x) when x ≠ π/2 and if lim(x→π/2) f(x) = f(π/2), find the value of k askedSep 12, in Limitsby Shyam01(504kpoints)05/03/ · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History


How Do You Find The Value Of Cos 2p Socratic



Find The Value Of Sin 11 Pi 3 Mathematics Stack Exchange
The trigonometric R method is a method of rewriting a weighted sum of sines and cosines as a single instance of sine (or cosine) This allows for easier analysis in many cases, as a single instance of a basic trigonometric function is often easier to work with than multiple are The R method is most often used to find the extrema (maximum and minimum) of combinations of trigonometricTextbook solution for Single Variable Calculus Concepts and Contexts, 4th Edition James Stewart Chapter 5 Problem 10P We have stepbystep solutions forThe value π is, in fact, the least such value of the wavenumber, and is associated with the fundamental mode of vibration of the string One way to show this is by estimating the energy , which satisfies Wirtinger's inequality 160 for a function f 0, 1 → ℂ with f (0) = f (1) = 0 and f , f ' both square integrable , we have
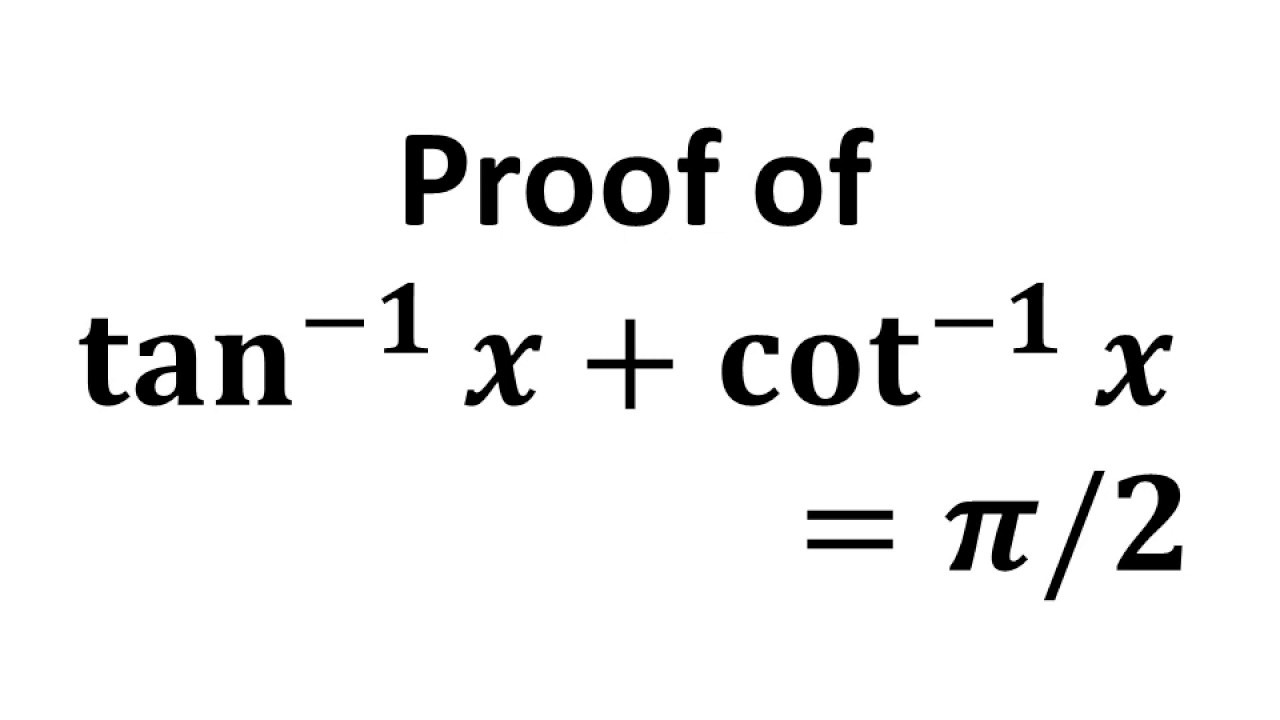


Tan 1 X Cot 1 X Pi 2 Arctan X Arccot X Pi 2 Youtube



If Sina 3 5 And Pi 2 A Pi Find Cos A Maths Trigonometric Functions Meritnation Com
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorIn your calculator to see what the factorial of onehalf is The result will be 06, and the exact answer is the square root of pi divided byEi(2nπ π/2) = cos (π/2 2nπ) isin (π/2 2nπ) = cos (π/2) isin (π/2) = i Hence i i has infinitely many values, e 2nπ π/2 for n any integer The valuse closest unity being approximately (, , 079, , ,)



Find The Exact Value Of Cos X 2 Given Cos X 1 4 And X In 0 Pi 2 Using Half Number Identities Youtube



Graph Of Y Tan X Video Trigonometry Khan Academy
05/02/21 · If cos (π/2 – u) = sin (π/8), find the value of variable u given that it lies between 0 and π/2 Solution Recall the cofunction identity for cosine and use it to assess the given trigonometric expressions cos (π/2 – u) = sin (u) cos (π/2 – u) = sin (π/8) u = π/8 Answer Therefore, the value of the variable u is π/8 Finding the Value of Angle Measure U Using CofunctionIf sec x cos 5x 1 = 0, where 0 < xA) force and power b) torque and energy c) torque and power d) force and torque 8 The dimensional formula of Planck's constant h is



If Sin 1 X Sin 1 Y 2pi 3 Then Value Of Cos 1 X Cos 1 Y Is
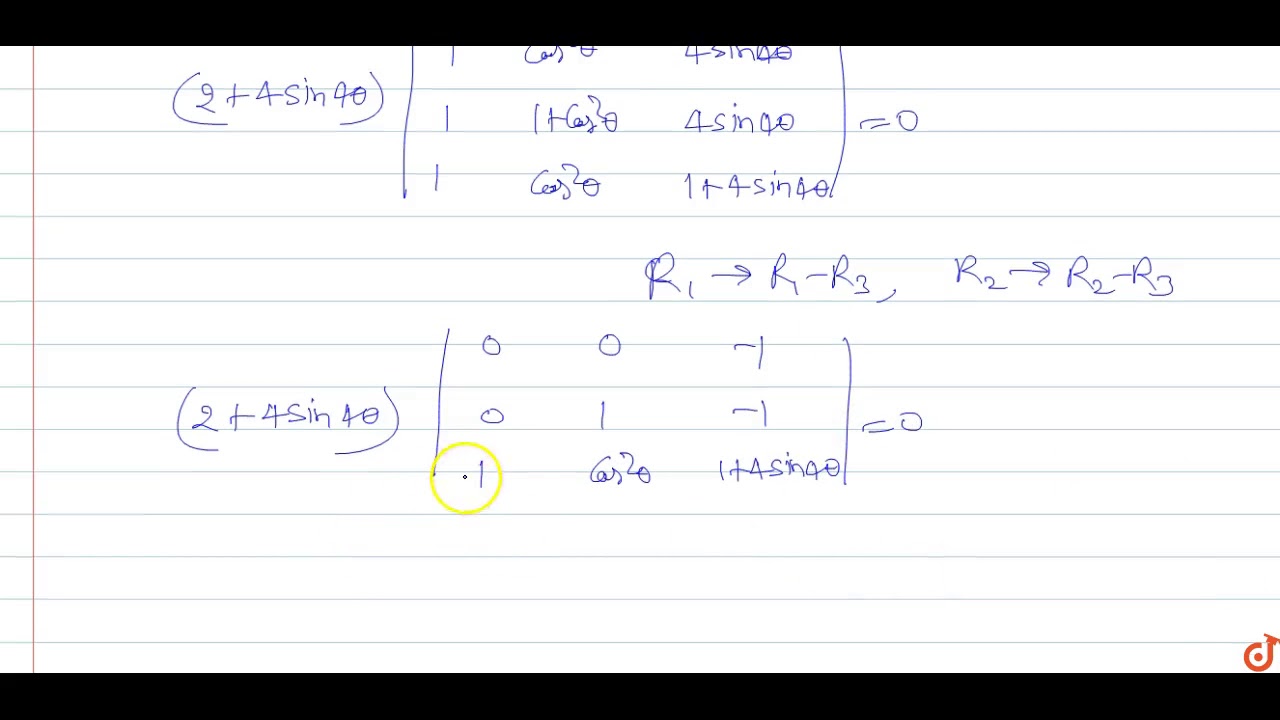


The Value Of Theta Lying Between Theta 0 And Theta Pi 2 And Satisfying The Equation 1 Youtube
31/01/21 · Find the approximate value for the function f(x) = cos (x) at x = π/2 using the linear approximation formula Use the result to approximate the value of cos(π/180) Solution Compute the tangent line equation to the given equation cos(x) at x = π/2 f(x) = cos(x) f(π/2) = cos(π/2) f(π/2) = 0 f'(x) = sin(x) f'(π/2) = sin(π/2) f'(π23/07/11 · Find the exact value under given conditions cos α = 12/13, π/2 < α < π sin β = 15/17, π/2 < α < π Find tan (α β)Evaluate limit X tends π/2 (secxtanx)
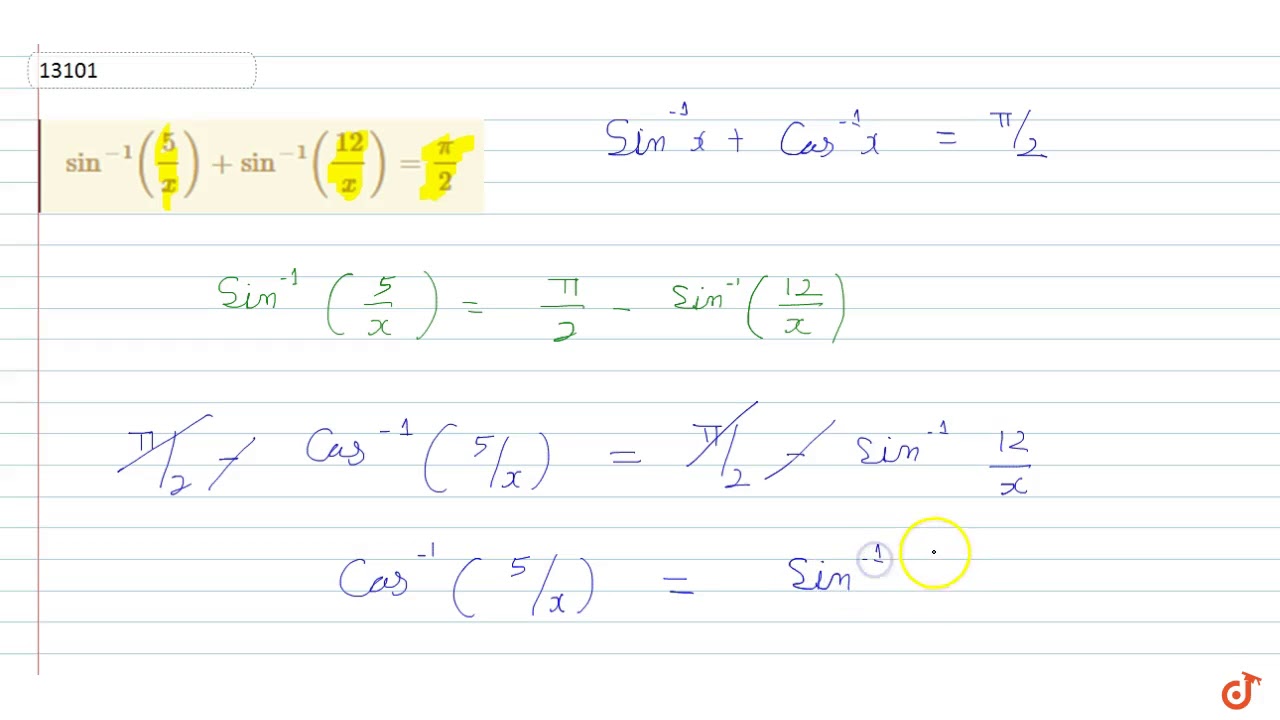


Sin 1 5 X Sin 1 12 X Pi 2 Youtube



How To Calculate The Area Of Circle In Terms Of Pi P Owlcation
Click here👆to get an answer to your question ️ The value of the integral ∫ 0 π/ 21 2cosx/( 2 cosx ) 2 d x isTom Ace pointed out that there is more about this in chapter 15 of Oystein Ore's Number Theory and Its History from 1948 and now available as a Dover book (19)Since it verifies the intermediate value theorem, there is a c (o, π/2) such that f(c) = 0 c sin c − 1 = 0 Therefore, there is at least one real solution to the equation x sin x − 1 = 0 Solution of exercise 12 f and g are two continuous functions in a, b and such that f(a) > g(a) and f(b) < g(b) Prove the existance of c withinin
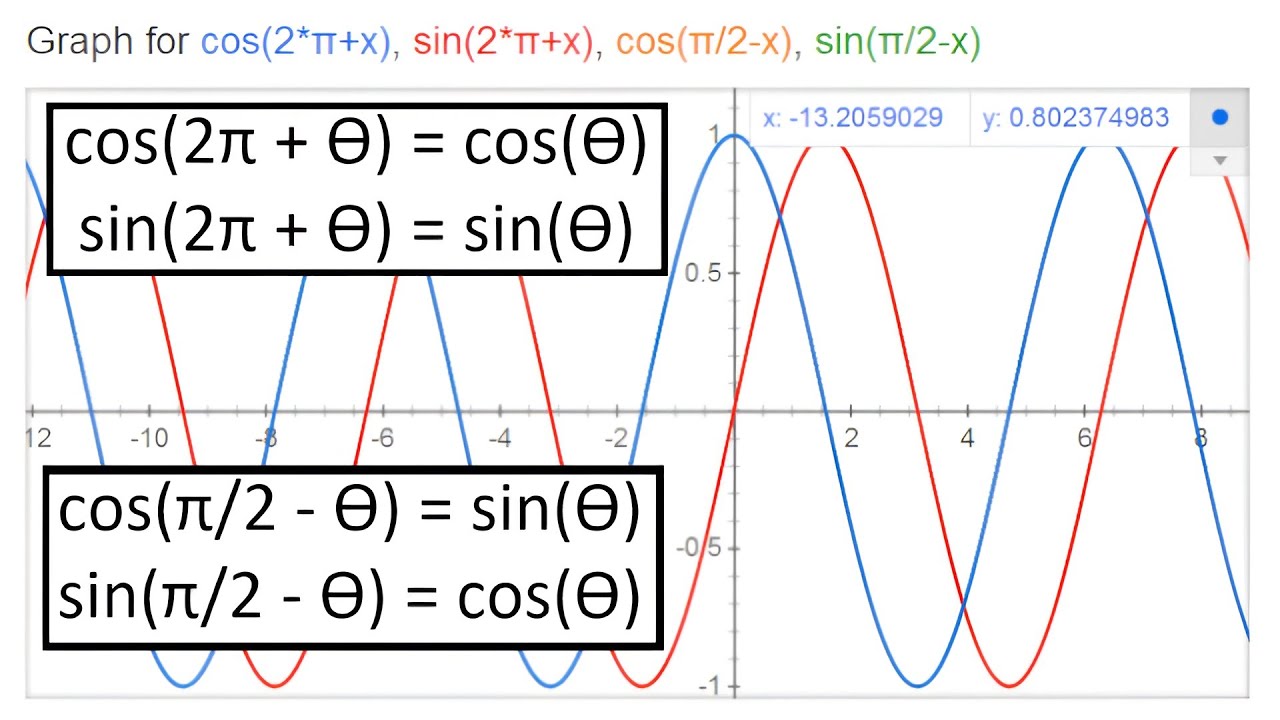


Trigonometry Identities Cos 2p X Sin 2p X Cos P 2 X Sin P 2 X Youtube



Calculate The Value Of Tan Pi 2 Pi 6 Brainly In
(π/2,3π/2) (b) Find the local maximum and minimum values of f Answer f0(x) = 0 when either cosx = 0 or sinx = −1, which is to say when x = π/2,3π/2 f0 changes from negative to positive at x = π/2 so, by the first derivative test, the local minimum value of f is f(π/2) = cos2(π/2)−2sin(π/2The point p lies on the curve with eqn x = (4y sin (2y)^2, given that p has coordinates (p,π/2), p is a constant, a) find the exact value of p;How do you use the reference angles to find #sin210cos330tan 135#?



If Tan X 512 And Pi2 X Pi Find The Values Of Tan 2x
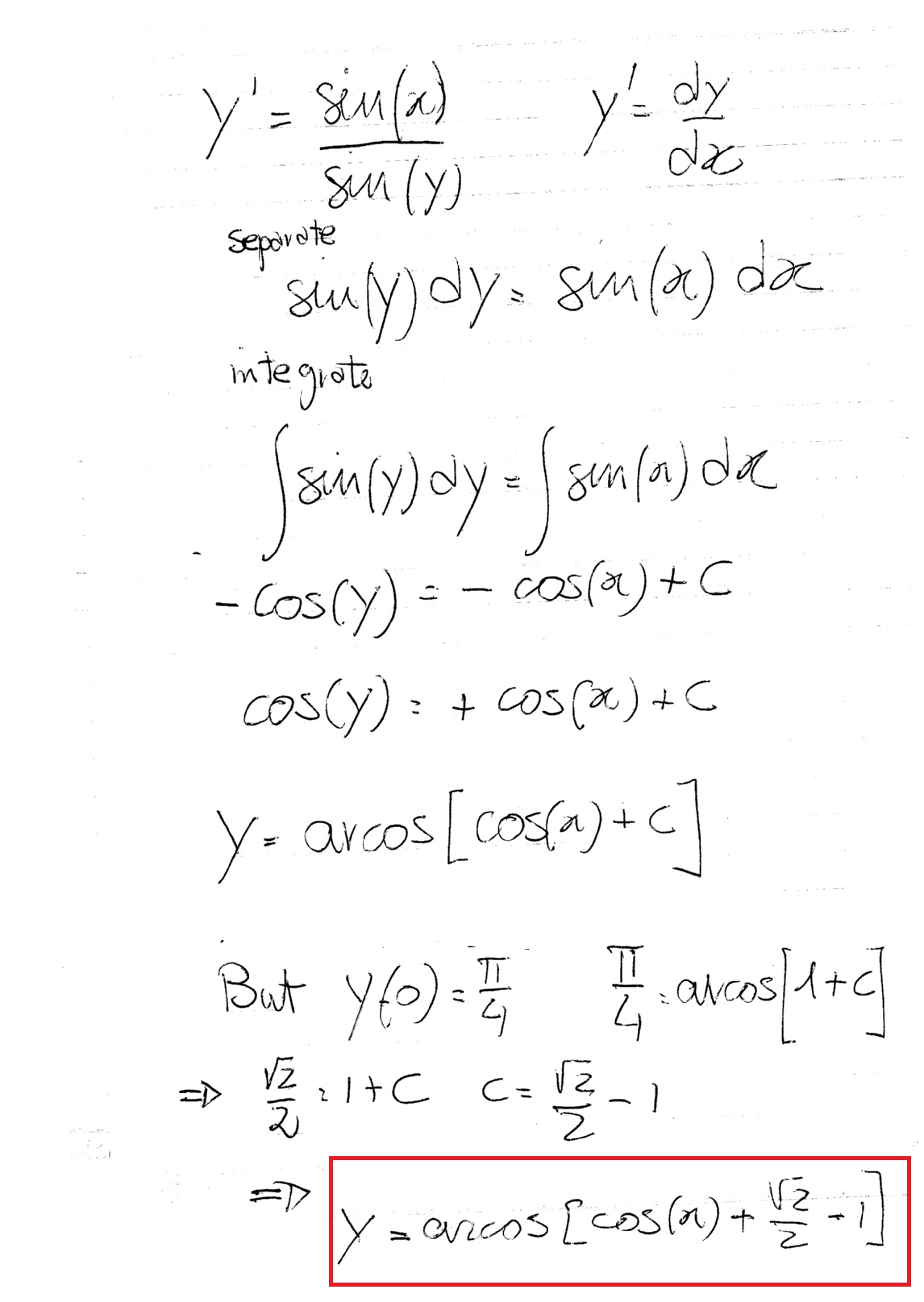


How Do You Solve The Initial Value Problem Y Sinx Siny Where Y 0 P 4 Socratic
Radians Preferred by Mathematicians Because the radian is based on the pure idea of "the radius being laid along the circumference", it often gives simple and natural results when used in mathematics For example, look at the sine function for very small valuesNotice also that sin θ = cos (π 2 − θ), sin θ = cos (π 2 − θ), which is opposite over hypotenuse Thus, when two angles are complementary, we can say that the sine of θ θ equals the cofunction of the complement of θ θ Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions Figure 6 From these relationships, the cofunction identities areWe found it a few days ago;



Ex 2 2 Find Sin Pi 3 Sin 1 1 2 Class 12 Ncert



Sec Pi 2 Theta Find The Value Brainly In
Did you see the "Careful!" column above?π /2 to π /2 (Note you can read more about Inverse Sine, Cosine and Tangent) Careful!


Cochranmath Primary Values



If Sin X 3 5 And 0 Lt X Lt Pi 2 Find The Valu
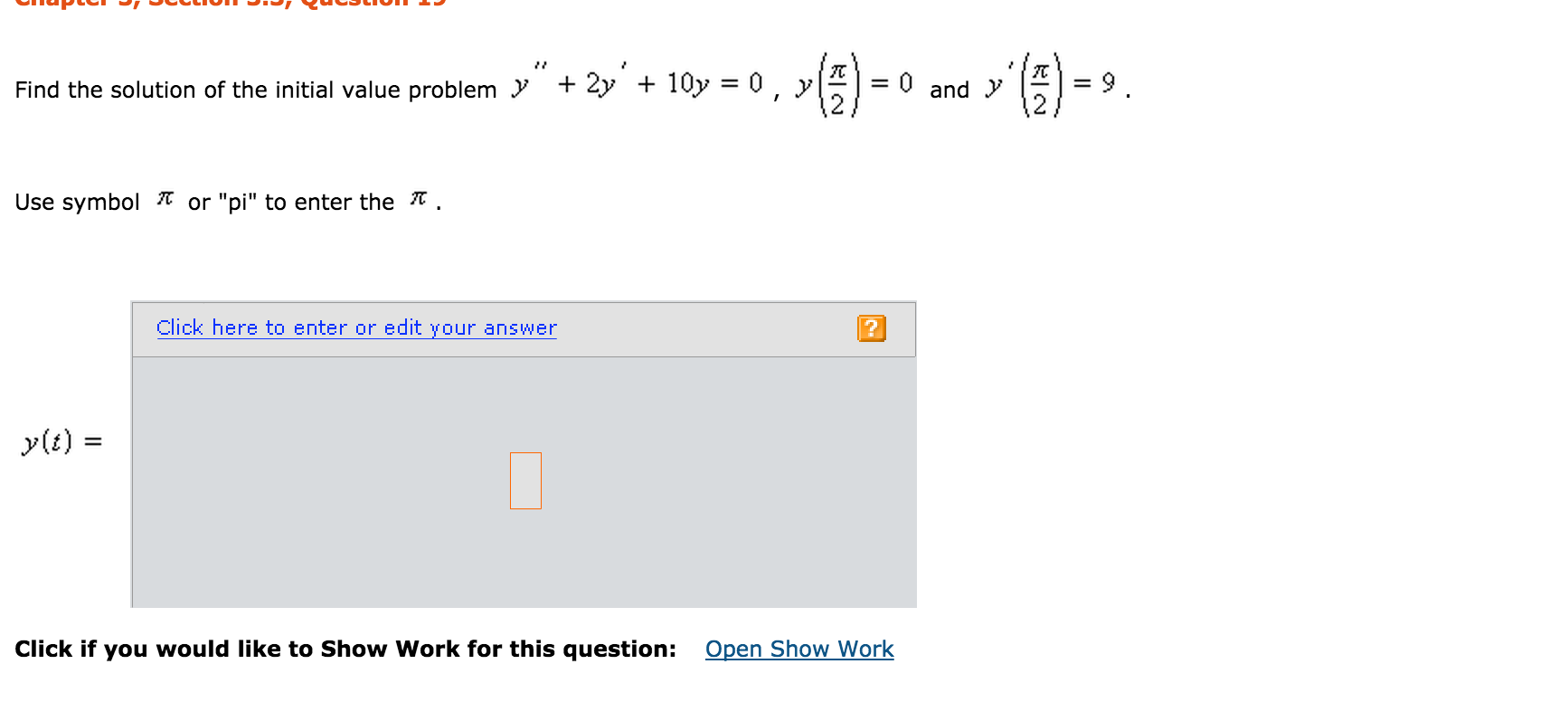


Solved Find The Solution Of The Initial Value Problem Y Chegg Com



Verify Lagranges S Mean Value Theorem For The Following Function F X Sin X On Left Dfrac Pi 2 Dfrac 5pi 2 Right



Warm Up Find The Values Of The Following Trig Functions Ppt Download



5 Ways To Calculate Pi Wikihow



Find The Value Of Cos 2 Pi 7 Cos 4 Pi 7 Cos 6 Pi 7 Youtube


What Is Pi And How Did It Originate Scientific American



The Value Of Int Pi 2 Pi 2 Dx X Sinx 4 Is Equal To



If Sin X Sqrt 5 3 And 0 Lt X Lt Pi 2 Find The Va



Given That Sin Theta 1 4 0 Theta P 2 What What Is The Exact Value Of Cos 8 Brainly Com



Find The Value Of X For Which Sec 1 X Sin 1 X Pi 2



The Value Of T A Nthetasin Pi 2 Theta Cos Pi 2 Theta Is 1 B


How Do You Prove Cos X Pi 2 Sin X Socratic



The Value Of Int 0 Pi 2 Frac Sin 3 X Sin X Cos X D X Is A Frac Pi 2 4 B Frac Pi 2 8 C Frac Pi 1 4 D Frac Pi 1 2



Ex 2 2 Find Sin Pi 3 Sin 1 1 2 Class 12 Ncert
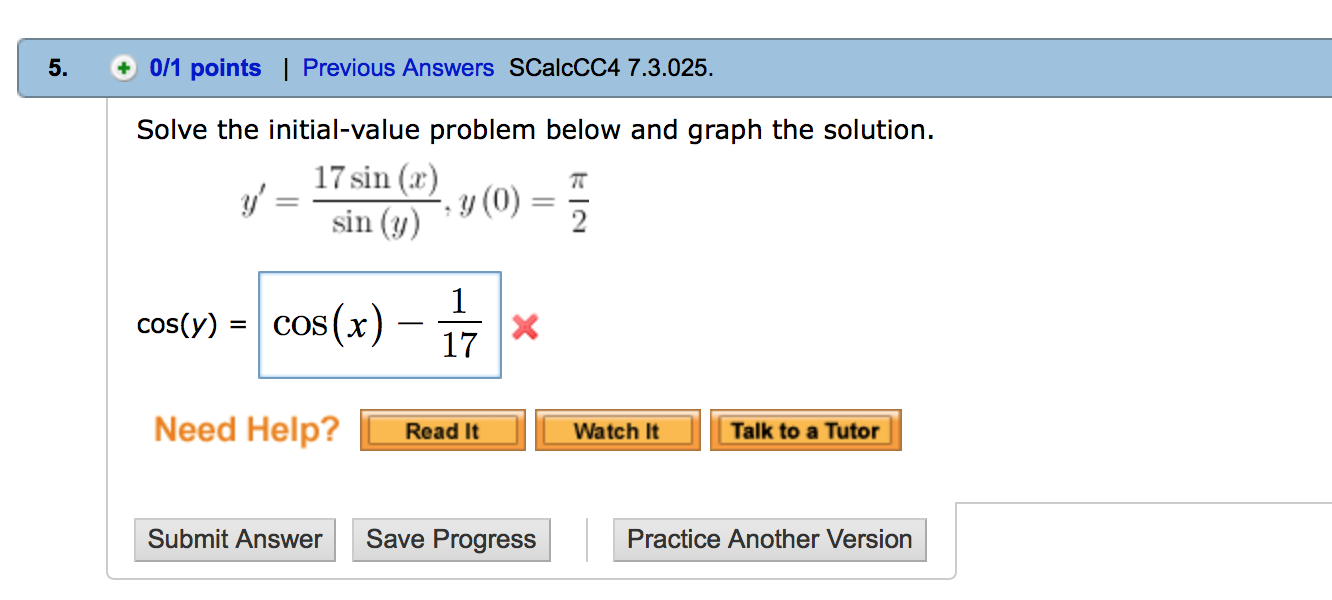


Solved Solve The Initial Value Problem Below And Graph Th Chegg Com


Solved Given The Log P Values Shown Below Calculate The Pi Value For The Bromine Group Course Hero



If Sin X 5 3 And 0 Lt X Lt P 2 Find The Value Of Sin 2x Cos 2x Tan 2x Brainly In



Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11


If X In 4n 1 Pi 2 4n 3 Pi 2 And N In N Then The Va



Ex 3 3 1 Prove Sin2 Pi 6 Cos2 Pi 3 Tan2 Pi 4 1 2
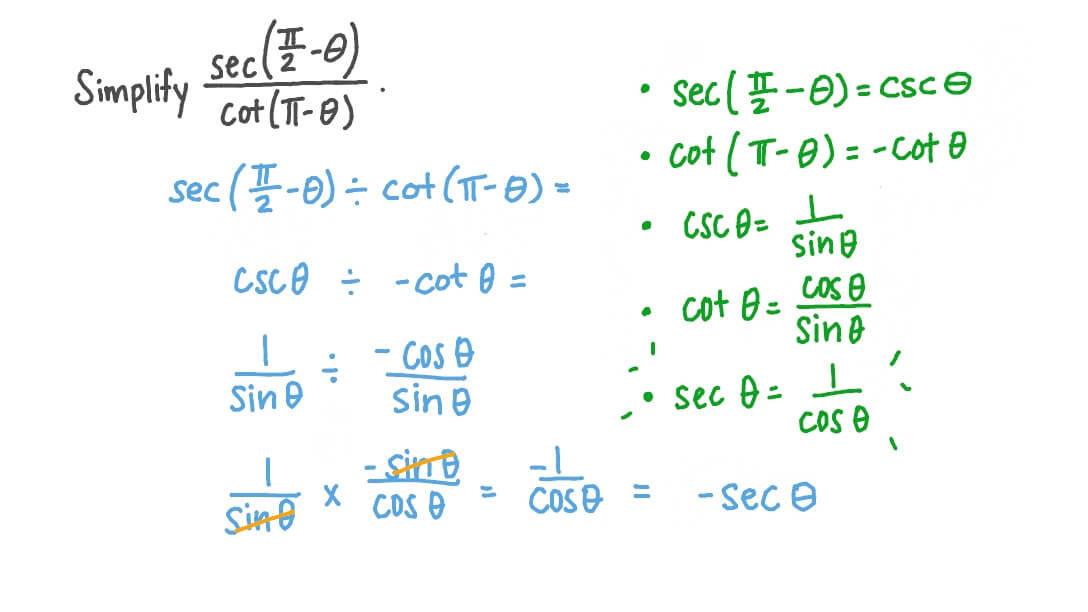


Question Video Using Periodic And Cofunction Identities To Simplify A Trigonometric Expression Nagwa



How N Pi 1 N Pi 6 N Pi Pi 6 And N Pi 1 N Pi 6 N Pi Pi 6 Mathematics Stack Exchange



The Value Of Int Pi 2 Pi 2 Sin 2 X 1 2 X Dx Is



Solve 11sin Theta 2 2 For A Value Of Theta When 0 Theta Pi 2 Socratic



The Value Of Cos Pi 2 2 Cos Pi 2 3 Cos Pi 2 10 Sin Pi 2 10 Is Youtube



Solved Pts Given The Signal 𝑥 𝑡 2 Cos 𝑡 𝑢 𝑡 Chegg Com



Sec 2 P 4 Sec 2 P 3 Cosec P 6 Cosec P 2 Find The Value Trigonometric Values Sci Pi



If Tan Inverse Root 3 Cot Inverse X P 2 Find The Value Of X Brainly In



The Value Of K For Which The Function F X 4 5 Tan4x Tan



Find Exact Value Of Cos 2 Pi 8 Youtube



Find The Value Of X In The Interval Pi 2 3pi 2 For Whic



The Value Of Dy Dx At X Pi 2 Where Y Is Given By Y



The Value Of Lim X Oo Int 0 Pi 2 Sin 2 M X D X Int 0 Pi 2



What Is Math Sqrt Pi Math Quora



If Sin X 5 3 And Pi2 X Pi Find The Value Of Cos X2



This Question Has Statement Which Is True Or False 5 If Pi 9 T



Barnett Practice Test 3 Extra Problems



Sin 2 Pi 6 Cos 2 Pi 3 Tan 2 Pi 4 1 2 Youtube



Transformation Of Cos X To Sin X Via Cos X Frac Pi 2 Sin X Mathematics Stack Exchange



Solved Let F X Y Sin 2x Y Find The Value Of The P Chegg Com



The Value Of Cos 𝜋 2 2 Cos 𝜋 2 3 𝑐𝑜𝑠 𝜋 2 10 Sin 𝜋 2 10 Is Youtube



What Is The Meaning Of This Expression Mathematics Stack Exchange
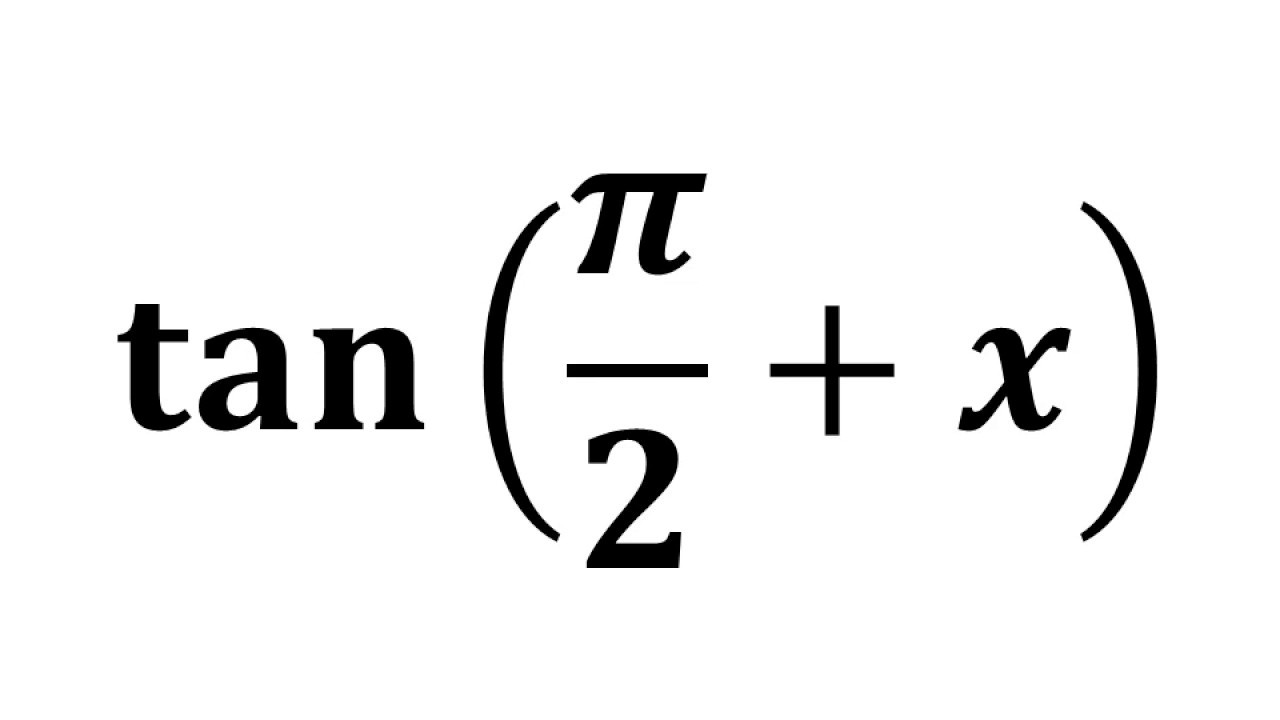


Tan Pi 2 X Tan Pi 2 Theta Youtube



Find All The Values Of Theta In Pi 2 Pi 2 Which Satisfy The



Find The Reduction Formula For Int 0 Pi 2 Sin N X Dx Youtube



Ex 2 2 15 If Tan 1 X 1 X 2 Tan 1 X 1 X 2 Pi 4



Solve Sin 1 1 X 2 Sin 1 X Pi 2 Then X Is Trigonometry
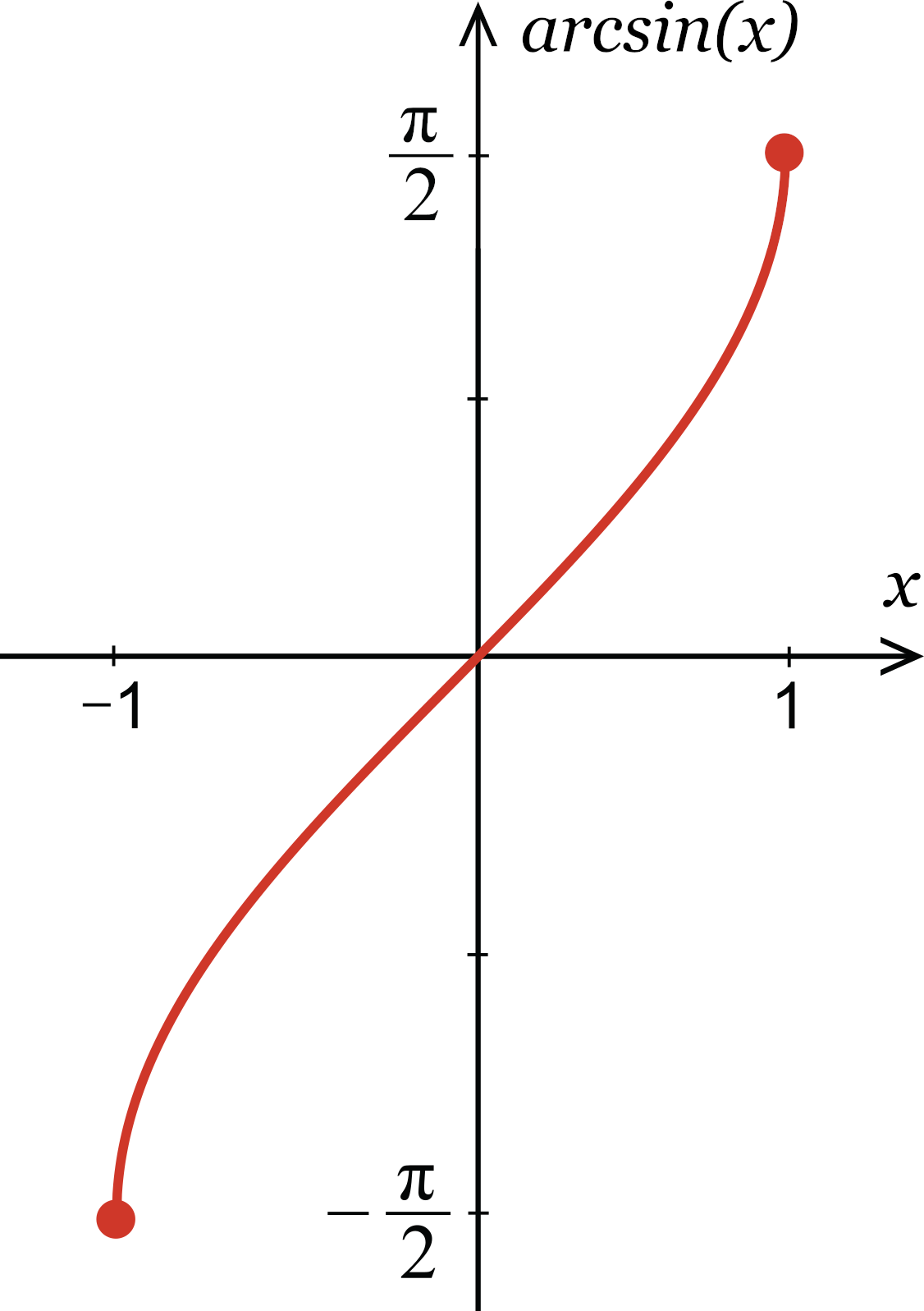


Inverse Sine Calculator Calculate Arcsin X Inch Calculator



If Sin Theta 4 5 And Pi Lt Theta Lt 3pi 2 Find T



Trigonometry Ppt Download



Solve Pi 2 Pi 2int X 3 X Cos X Tan 5 X 1 Dx



If 2sin Theta Pi 3 Cos Theta Pi 3 And Tantheta 3 0 Find The Value Of Theta



Unclear Why The Highest Argument Value For Cosine Function Cos X Frac Pi 4 Is Frac Pi 2 Mathematics Stack Exchange
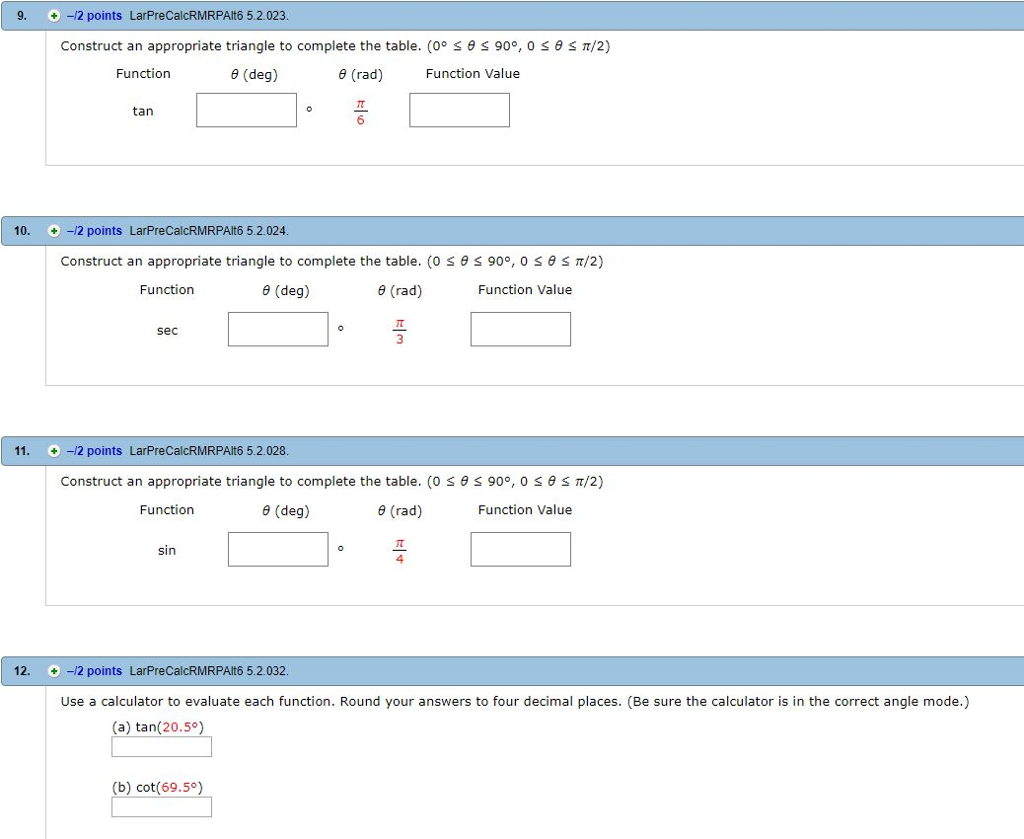


Solved 9 2 Points Larprecalcrmrpalt6 5 2 023 Construct Chegg Com
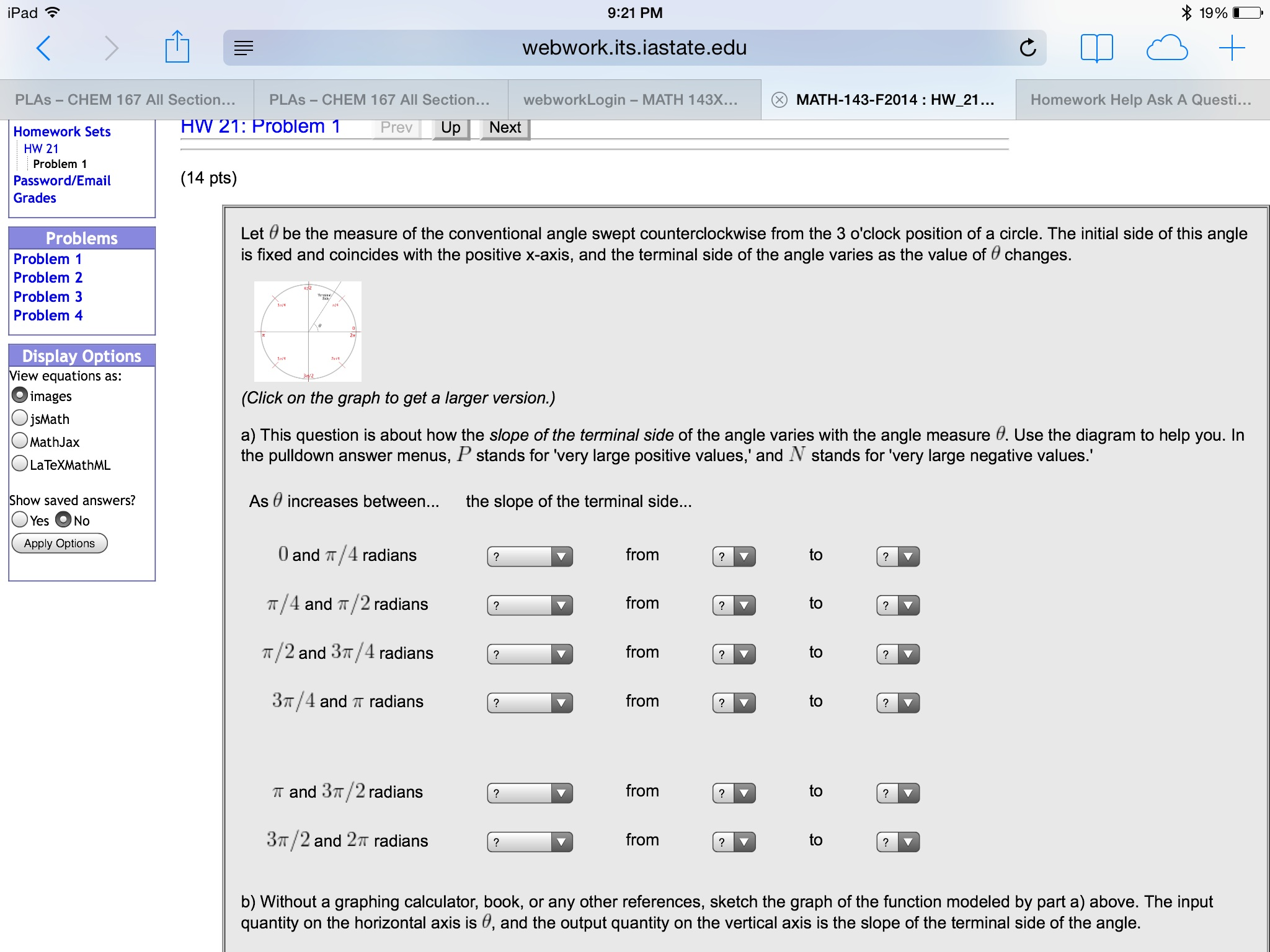


Solved Let Theta Be The Measure Of The Conventional Angl Chegg Com



The Value Of Theta Lying Between Pi 4 And Pi 2 And 0leale Pi 2 And Satisfying Youtube



The Value Of Int Pi 4 Pi 2 Sinx 2x Pi Dx Where Den



The Value Of Cos 1 1 Sin 1 1 Is A Pi B Pi 2 C
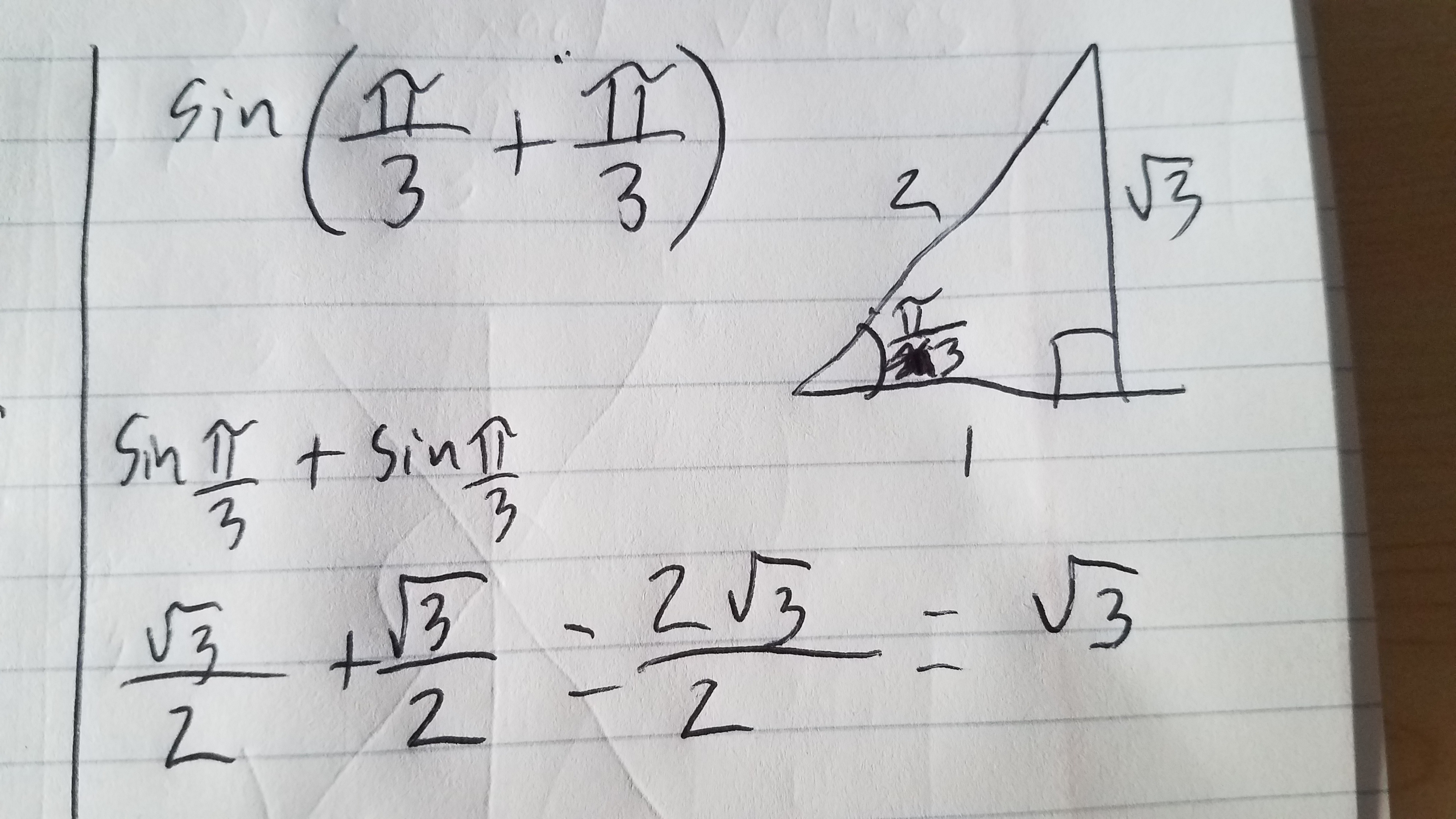


Answered Evaluate In Exact Values Sin P 6 Bartleby
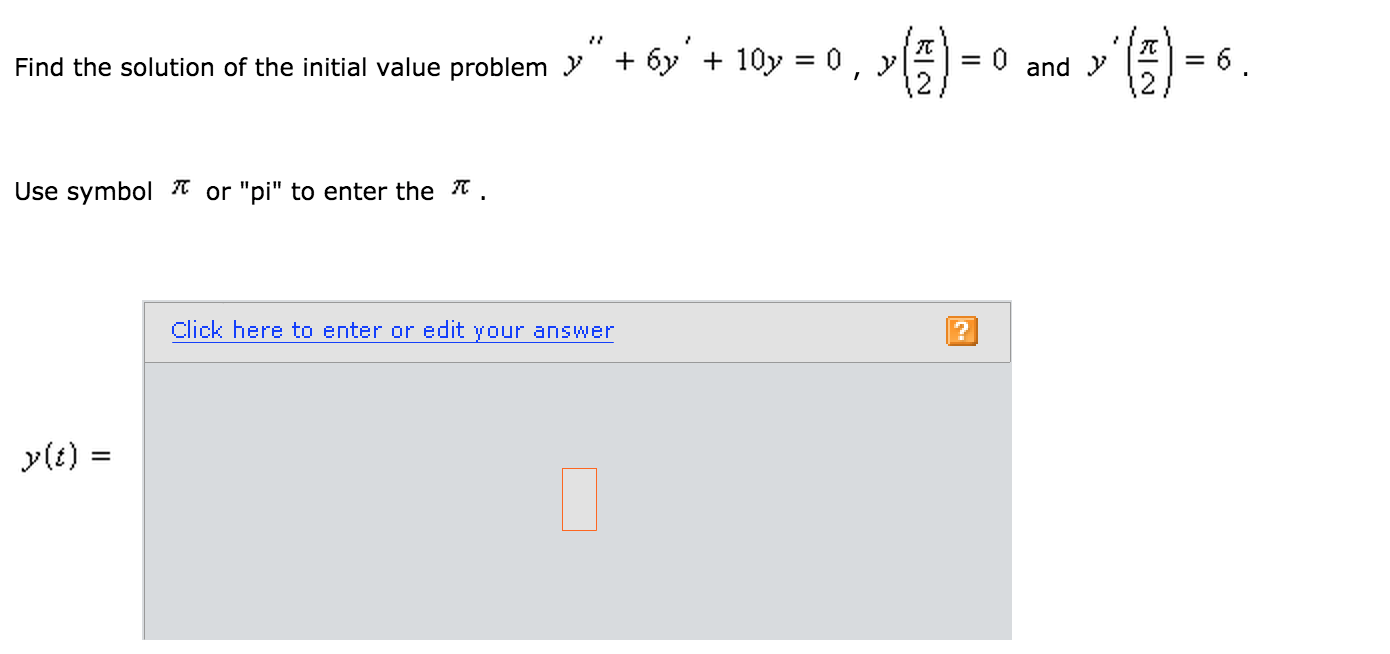


Solved Find The Solution Of The Initial Value Problem Y Chegg Com



Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11



P 2 P 2 X Dx 8 Cos 2 2x 1 Has The Value A P 2 6 B P 2 12 C P 2 24 D None Of These Youtube



If Cosa Cosb 1 3 Where P 2 Lt A Lt P And P Lt B Lt 3p 2 Then Find The Value Of Tana Brainly In



If 2sinx 1 Pi 2 X Pi And Sqrt2 Cos Y 1 3pi 2 Y 2pi F
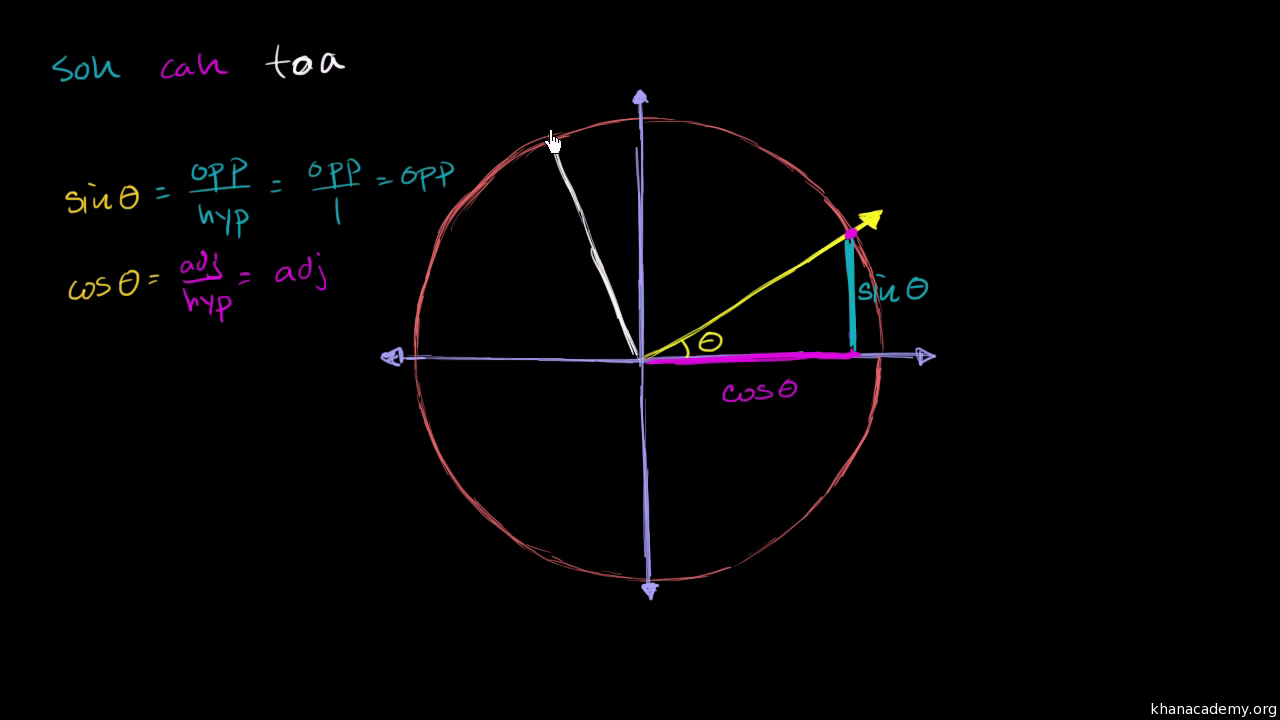


Sine Cosine Identities Periodicity Video Khan Academy



The Minimum Value Of F X Sin X Cos X In 0 P 2 Is



0 件のコメント:
コメントを投稿